Introdução à Física Computacional

Objetivo do minicurso:

Ao final deste curso, os participantes deverão:

Entender o papel da física computacional na resolução de problemas.
Conhecer a interface básica e principais comandos do Octave.
Resolver problemas simples de física utilizando simulação computacional.

Duração média: 1h40min

Estrutura do minicurso:

Uso de algoritmos e computadores para resolver problemas físicos.

Introdução ao Octave.
Familiarização com o ambiente e a interface.
Demonstração rápida de comandos básicos.

Variáveis e operações aritméticas.
Vetores e matrizes.

Exercício: Movimento Retilíneo Uniforme.
Funções básicas (ex.: sin, cos, exp, sqrt).

Exercício: Movimento Harmônico Amortecido.
Os exercícios incluem:

Gráficos.
Resolução de problemas e outros exemplos.

Exercício: campo gravitacional de dois buracos negros.
Exercício: pêndulo duplo em movimento caótico.

Uso de algoritmos e computadores para resolver problemas físicos...

Tal uso permite resolver problemas complexos e simular fenômenos naturais que desafiam a matemática ou o cálculo tradicional, possibilitando análises precisas e avanços em diversas áreas científicas.

Introdução ao Octave

Octave é uma ferramenta de código aberto para cálculos numéricos, muito utilizada como alternativa ao MATLAB, que permite realizar operações matemáticas, simulações e visualizações de dados de forma eficiente.

Familiarização com o ambiente e a interface

O ambiente Octave inclui uma interface de linha de comando ou GUI (Interface Gráfica do Usuário), onde é possível escrever e executar códigos, visualizar gráficos e manipular dados. Ele possui um editor de scripts integrado, ferramentas para plotagem e bibliotecas de funções matemáticas, facilitando o desenvolvimento, teste e visualização de simulações numéricas.

Demonstração rápida de comandos básicos

Na "Janela de Comandos" escreva, apetando <enter> após digitar cada sentença a seguir:

2+3

4*4

2^3

Se você colocar um ponto e vírgula ";" no final da sentença, ele faz o cálculo, mas não te mostra o resultado:

2+3;

Para ver o resultado, digita a palavra "ans":

ans

Variáveis e operações aritméticas

Uma variável é representada por uma letra que pode ser seguida de números. Por exemplo, podemos definir a variável x, atribuindo o valor 5 para ela:

x = 5;

O Octave guardará esse valor. Você pode fazer um cálculo com ele:

x+3

Confira o valor de x:

Agora defina y:

y = 4*x

Modifique o valor de x:

x = 1

Verifique se y mudou:

Faça uma subtração:

z = x - y

E uma exponenciação:

m = y^2

E agora uma divisão:

n = y/z

Vetores e matrizes

Um vetor linha é uma sequência de elementos dispostos horizontalmente:

v1 = [1, 2, 3, 4, 5];

Um vetor coluna é uma sequência de elementos dispostos verticalmente:

v2 = [1; 2; 3; 4; 5];

É possível criar vetores com uma sequência de números usando um incremento específico:

v3 = 1:2:9; % Vetor linha de 1 a 9 com incremento de 2
v4 = 0:0.5:2; % Vetor linha de 0 a 2 com incremento de 0.5

Note que o que está escrito após "%" é um comentário que não interfere no código.

Soma de vetores. Copie:

v1 = [1, 2, 3];

v2 = [4, 5, 6];

v_sum = v1 + v2

Subtração:

v_diff = v1 - v2

Multiplicação elemento a elemento:

v_mult = v1 .* v2

Divisão elemento a elemento:

v_div = v1 ./ v2

Multiplicação por escalar:

a = 2;

v3 = a*v1;

Verifique os valores:

Exercício: Movimento Retilíneo Uniforme (MRU)

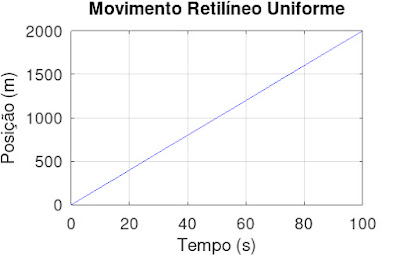
Um carro está se movendo em uma estrada reta com uma velocidade constante de v = 20 m/s. Ele parte da posição zero no tempo zero. Utilize o Octave para calcular e plotar a posição do carro em função do tempo para um intervalo de tempo de 0 a 100 segundos.

Sendo assim, nós teremos:

x0 = 0; % Posição inicial em metros

v = 20; % Velocidade constante em m/s

t_final = 10; % Tempo final em segundos

Copie as três linhas de código acima, abra o "Editor" do Octave e cole-as.

Salve essa rotina como um arquivo com nome "MRU.m".

Continue com o editor aberto, editando o arquivo.

Agora, precisamos inserir a equação do movimento x = x0 + v * t. Contudo, antes, precisamos definir o tempo t indo de 0 até 100 segundos.

Então, ele será um vetor com valores de 0 a 100.

Assim, abaixo da terceira linha cole os comandos:

t = linspace(0, t_final, 100); % 100 pontos de tempo de 0 a 10 segundos

x = x0 + v * t; % Calculando a posição para cada instante de tempo

Agora, vamos inserir os comandos para gerar (plotar) um gráfico de tempo versus posição:

% Plotando a posição em função do tempo figure;

plot(t, x, 'b-');

xlabel('Tempo (s)');

ylabel('Posição (m)');

title('Movimento Retilíneo Uniforme');

grid on;

Você deverá obter um gráfico similar a este:

Funções básicas

São alguns exemplos (copie e cole) :

sqrt(16);     % Raiz quadrada
sin(pi/2);    % Seno
exp(1);       % Exponencial
log(10);      % Logaritmo natural

Exercício: Oscilador Harmônico Amortecido

Código em Octave:

% Dados do problema
m = 1;    % Massa (kg)
b = 2;    % Coeficiente de amortecimento (Ns/m)
k = 100; % Constante da mola (N/m)
A = 1;    % Amplitude inicial (m)

% Cálculo da frequência angular natural e da razão de amortecimento
omega_0 = sqrt(k / m);
zeta = b / (2 * sqrt(m * k));

% Cálculo da frequência angular amortecida
omega_d = omega_0 * sqrt(1 - zeta^2);

% Tempo para plotagem
t = linspace(0, 20, 1000); % Intervalo de 0 a 20 segundos

% Cálculo do deslocamento
x = A * exp(-zeta * omega_0 * t) .* cos(omega_d * t);

% Exibindo o gráfico
figure;
plot(t, x, 'b-');
xlabel('Tempo (s)');
ylabel('Deslocamento (m)');
title('Oscilador Harmônico Amortecido');
grid on;

Resultados:

Você vai obter um gráfico que te dá todas as posições x de oscilação do amortecedor em função do tempo t:

Exercício: campo gravitacional de dois buracos negros

Código em Octave (dois buracos negros):

% Constante gravitacional e massas dos buracos negros
G = 6.674e-11; % Constante gravitacional (m^3 kg^-1 s^-2)
M1 = 5e30;      % Massa do buraco negro 1 (kg)
M2 = 3e30;      % Massa do buraco negro 2 (kg)

% Posições dos buracos negros
x1 = -2; y1 = 0; % Coordenadas do buraco negro 1
x2 = 2; y2 = 0;   % Coordenadas do buraco negro 2

% Criação da malha de pontos no plano bidimensional
[x, y] = meshgrid(linspace(-5, 5, 100), linspace(-5, 5, 100));

% Distâncias dos pontos da malha até cada buraco negro
r1 = sqrt((x - x1).^2 + (y - y1).^2);
r2 = sqrt((x - x2).^2 + (y - y2).^2);

% Cálculo da aceleração gravitacional resultante
g1 = G * M1 ./ (r1.^2); % Campo gravitacional do buraco negro 1
g2 = G * M2 ./ (r2.^2); % Campo gravitacional do buraco negro 2

% Somando os campos para obter o campo gravitacional total
g_total = g1 + g2;

% Tratando o infinito nos locais dos buracos negros
g_total(r1 == 0) = NaN;
g_total(r2 == 0) = NaN;

% Exibindo o gráfico da superfície do campo gravitacional total
figure;
mesh(x, y, -g_total); % Usando valores negativos para criar o efeito de "poço"
xlabel('x (m)');
ylabel('y (m)');
zlabel('Aceleração Gravitacional (m/s^2)');
title('Superfície da Aceleração Gravitacional de Dois Buracos Negros');
colorbar; % Adiciona uma barra de cor para referência

Exercício: pêndulo duplo em movimento caótico

% Parâmetros do pêndulo duplo
L1 = 1;             % Comprimento do primeiro pêndulo (m)
L2 = 1;             % Comprimento do segundo pêndulo (m)
m1 = 1;             % Massa do primeiro pêndulo (kg)
m2 = 1;             % Massa do segundo pêndulo (kg)
g = 9.81;           % Aceleração gravitacional (m/s^2)

% Parâmetros da simulação
dt = 0.01;          % Passo de tempo (s)
T = 20;             % Tempo total de simulação (s)
n_steps = T / dt;   % Número total de passos

% Condições iniciais
theta1 = pi / 2;       % Ângulo inicial do primeiro pêndulo (rad)
theta2 = pi / 2;       % Ângulo inicial do segundo pêndulo (rad)
omega1 = 0.0;          % Velocidade angular inicial do primeiro pêndulo (rad/s)
omega2 = 0.0;          % Velocidade angular inicial do segundo pêndulo (rad/s)

% Função para calcular as derivadas
function dY = double_pendulum_derivatives(Y, g, L1, L2, m1, m2)
    theta1 = Y(1);
    omega1 = Y(2);
    theta2 = Y(3);
    omega2 = Y(4);

    delta_theta = theta2 - theta1;

    % Equações de movimento do pêndulo duplo
    denom1 = (m1 + m2) * L1 - m2 * L1 * cos(delta_theta) * cos(delta_theta);
    denom2 = (L2 / L1) * denom1;

    dtheta1 = omega1;
    domega1 = (m2 * L1 * omega1^2 * sin(delta_theta) * cos(delta_theta) + m2 * g * sin(theta2) * cos(delta_theta) + m2 * L2 * omega2^2 * sin(delta_theta) - (m1 + m2) * g * sin(theta1)) / denom1;

    dtheta2 = omega2;
    domega2 = (-m2 * L2 * omega2^2 * sin(delta_theta) * cos(delta_theta) + (m1 + m2) * g * sin(theta1) * cos(delta_theta) - (m1 + m2) * L1 * omega1^2 * sin(delta_theta) - (m1 + m2) * g * sin(theta2)) / denom2;

    dY = [dtheta1; domega1; dtheta2; domega2];
end

% Preparação para o gráfico
figure;
hold on;
xlabel('Posição x (m)');
ylabel('Posição y (m)');
title('Trajetória do Pêndulo Duplo com Cores Variáveis');
axis equal;
axis([-2 * (L1 + L2), 2 * (L1 + L2), -2 * (L1 + L2), 2 * (L1 + L2)]);

% Loop para resolver as EDOs e plotar a trajetória
for k = 1:n_steps
    % Estado atual
    Y = [theta1; omega1; theta2; omega2];

    % Método de Runge-Kutta de 4ª ordem
    k1 = double_pendulum_derivatives(Y, g, L1, L2, m1, m2) * dt;
    k2 = double_pendulum_derivatives(Y + 0.5 * k1, g, L1, L2, m1, m2) * dt;
    k3 = double_pendulum_derivatives(Y + 0.5 * k2, g, L1, L2, m1, m2) * dt;
    k4 = double_pendulum_derivatives(Y + k3, g, L1, L2, m1, m2) * dt;

    % Atualização das variáveis de estado
    Y = Y + (k1 + 2 * k2 + 2 * k3 + k4) / 6;
    theta1 = Y(1);
    omega1 = Y(2);
    theta2 = Y(3);
    omega2 = Y(4);

    % Calculando as coordenadas x e y dos pêndulos
    x1 = L1 * sin(theta1);
    y1 = -L1 * cos(theta1);
    x2 = x1 + L2 * sin(theta2);
    y2 = y1 - L2 * cos(theta2);

    % Definindo a cor gradualmente usando o matiz do HSV
    hue = mod(k / n_steps, 1);   % Varre o matiz de 0 a 1 sem branco
    color = hsv2rgb([hue, 1, 1]); % Converte o matiz para RGB

    % Plotando a posição da ponta do segundo pêndulo com cor variável
    plot(x2, y2, '.', 'Color', color);
    drawnow;          % Atualiza o gráfico em tempo real
    pause(0.01);      % Delay para a animação
end

hold off;

FIM

Pesquisar neste blog

Blog pessoal do Elvis